まず基本概念から。
コホート研究…ある要因の暴露群と非暴露群とを用意して、一定期間後に何かしらの疾病になるかならないかを調べる(例えばヨーグルトを毎日食べた人が10年後に大腸がんになるか否か)。これをグラフ化すると下のようになる。

暴露した群が疾病にかかるリスク(=イベントの発生率)は a/(a+b)
暴露していない群が疾病にかかるリスクは c/(c+d)
ここでリスク比=相対危険度=相対リスクは、暴露した群と暴露しなかった群の疾病のかかりやすさの比を表すので、{a/(a+b)} / {c/(c+d)}
また、リスク差=寄与危険度=絶対リスクは、暴露した群と暴露しなかった群の疾病のかかりやすさの差をとったものとなるので、{a/(a+b)}-{c/(c+d)}
例えば、あるサプリメントAを飲んだ群100人のうち2人が疾病Bにかかり、Aを飲んでない群100人のうち5人がBにかかったとする。このとき暴露群のリスクは2%、非暴露群では5%なので、リスク比は0.4 =40%になる。つまりAを飲むことによってBのリスクが40%減ることになる。しかし、リスク差をとってみると5%-2%で3%、つまり3%しか減っていない、ともいえる。このように、どちらも正しいけれど、相対リスクと絶対リスクとの間にかなりの印象の差があったりする。
続いて、患者対象研究。
患者対象研究…ある疾病にかかっている人とかかっていない人を用意する。この人たちが過去に何かしらの要因に暴露していたかどうかを調べる。
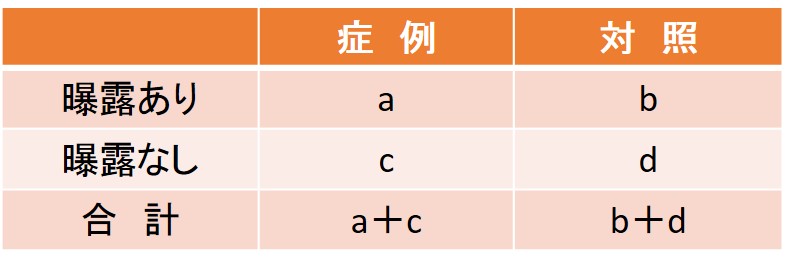
この方法の優れているところは、まれな疾患でも調査可能ということ。要因Aと疾病Bとの関連を調べたいと思ってコホート研究を行っても、まれすぎてどちらも0人、なんてこともあるかもしれない。しかし患者対象研究であれば、患者を100人、それ以外を100人持ってきて過去の曝露要因を調べればよい。となれば、このグラフにおいてa+bとか、c+dという数字には何の意味もないことが分かる、と思う(なぜなら元々まれな疾患にかかっている人を集めてきているのだから、aやcの数はかなり多くなっているはず)。つまりリスク比が使えない。ここでオッズ比の登場。
オッズについていろいろ考えてしまうとよく分からなくなるので、ここはオッズ=曝露の比という風に覚えておいていいのでは。つまり症例におけるオッズはa/c(割合じゃないので、a/a+cではない!)、対照におけるオッズはb/d、よってオッズ比は{a/c} / {b/d}=ad/bcとなる。
ここで、ある疾病が十分に小さい割合であるとする。すると相対危険度={a/(a+b)} / {c/(c+d)}においてa+bはbに、c+dはdにそれぞれ近似できる。よって相対危険度={a/b} / {c/d}=ad/bcとなり、患者対象研究におけるオッズ比はリスク比に近似できることになる。